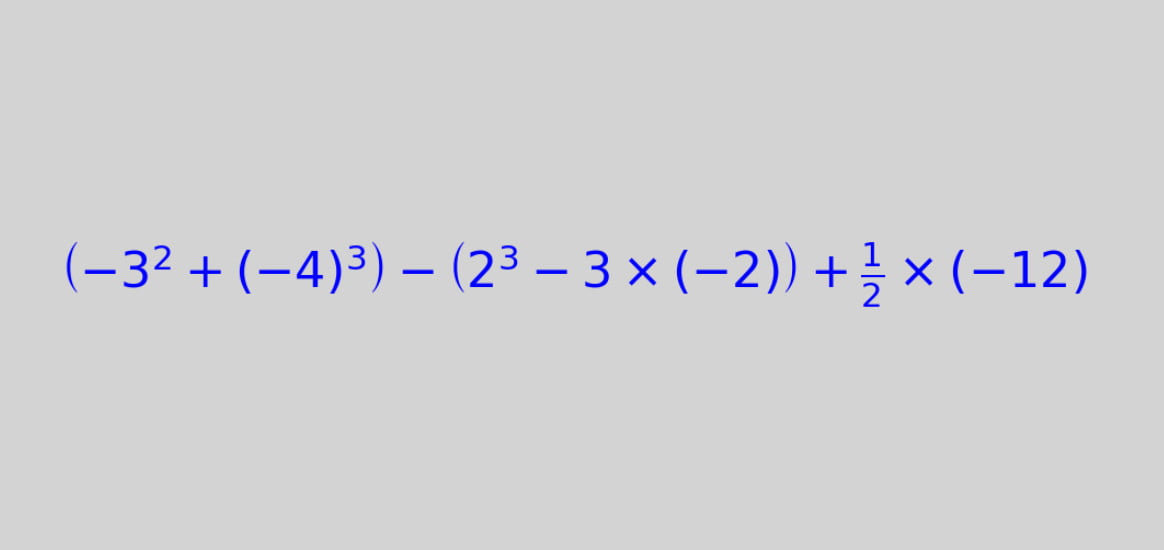To wyrażenie to doskonały test umiejętności matematycznych, który pokazuje, jak skomplikowane może być rozwiązanie, nawet jeśli na pierwszy rzut oka wydaje się być tylko zbiorem podstawowych operacji.
Zapraszamy na grupę – Zagadki, quizy oraz testy i łamigłówki
Działanie: \((-3^2 + (-4)^3) – (2^3 – 3 \times (-2)) + \frac{1}{2} \times (-12)\)
Polecamy – Układanie ułamków – Puzzle
Przyjrzyjmy się temu krok po kroku
Działanie: \((-3^2 + (-4)^3) – (2^3 – 3 \times (-2)) + \frac{1}{2} \times (-12)\)
Krok 1: Potęgowanie i działanie w nawiasach
Obliczamy \(-3^2\), co daje \(-9\), a następnie \((-4)^3\), co daje \(-64\). Suma tych dwóch wyników to \(-73\).
W drugim wyrażeniu obliczamy \(2^3\), co daje \(8\), a po mnożeniu \(3\) przez \(-2\), otrzymujemy \(-6\). Różnica tych dwóch wyników \(8 – (-6)\) to \(14\).
Krok 2: Działanie na ułamkach i mnożenie
Mnożymy \(\frac{1}{2}\) przez \(-12\), co daje \(-6\).
Krok 3: Końcowe dodawanie i odejmowanie
Dodajemy i odejmujemy uzyskane wyniki: \((-73) – 14 + (-6) = -93\).
Wynik
Ostateczny wynik działania to \(-93\).
Analiza Wyniku:
Ostateczny wynik działania matematycznego to −93. To wyrażenie jest świetnym przykładem na to, jak ważna jest dokładność i zrozumienie kolejności operacji, a także wpływ znaków na wynik końcowy. Nawiasy zmieniają kolejność wykonywania działań, co jest kluczowe do uzyskania poprawnego wyniku w bardziej złożonych wyrażeniach matematycznych.
Rozwiązanie tego zadania pokazuje, jak matematyka może być zarówno piękna, jak i skomplikowana. Demonstruje znaczenie posiadania solidnych podstaw matematycznych i umiejętność stosowania ich w praktyce. Każdy krok, od potęgowania po operacje na ułamkach, wymaga uwagi i precyzji, podkreślając, jak ważne jest zrozumienie podstawowych zasad matematycznych i ich zastosowanie w bardziej złożonych sytuacjach.
Podsumowanie
To rozwiązanie krok po kroku pokazuje, jak rozkładając złożone wyrażenie matematyczne na mniejsze części i skupiając się na jednym kroku na raz, możemy dokładnie obliczyć i zrozumieć wynik końcowy. Każdy krok wymaga uważności i zastosowania odpowiednich zasad matematycznych, co czyni matematykę nie tylko narzędziem do obliczeń, ale także sposobem na rozwijanie logicznego myślenia i rozwiązywanie problemów.