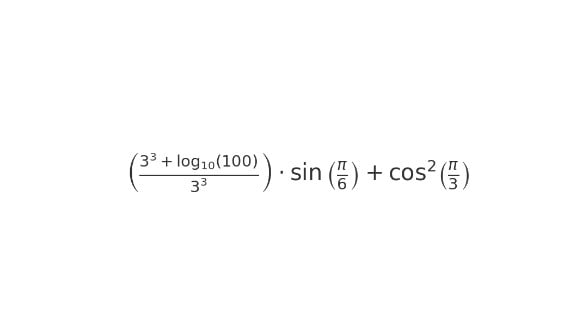Rozwiązywanie tej zagadki to doskonały sposób na naukę poprzez praktykę. Daje ono okazję do eksploracji matematycznych koncepcji w kontekście rzeczywistym, zachęcając do myślenia krytycznego i zastosowania wiedzy w sposób kreatywny i innowacyjny. Każdy krok rozwiązania stanowi odrębną lekcję, pokazując, jak różne elementy matematyki łączą się, by tworzyć spójne i logiczne całości.
\((\frac{3^3 + \log_{10}(100)}{27}) \cdot \sin(\frac{\pi}{6}) + \cos^2(\frac{\pi}{3})\)
To zadanie nie tylko sprawdza umiejętności matematyczne, ale również rozwija intuicję liczbową i zrozumienie, jak matematyka otacza nas w codziennym życiu, będąc fundamentem rozwiązywania problemów. Jest to zaproszenie do pogłębienia wiedzy matematycznej i odkrycia, jak potężne i piękne mogą być liczby, gdy tylko zaczniemy je rozumieć.
To działanie matematyczne, składające się z potęgowania, logarytmów, funkcji trygonometrycznych oraz operacji dodawania i mnożenia, stanowi doskonałą zagadkę matematyczną, która może być używana jako narzędzie edukacyjne. Przedstawia ono unikalną okazję do eksploracji różnych dziedzin matematyki w jednym zadaniu, co sprzyja zrozumieniu i przyswajaniu wiedzy na wielu poziomach.
Zaawansowane Działanie Matematyczne: Rozwiązanie krok po kroku
Wyrażenie: \((\frac{3^3 + \log_{10}(100)}{27}) \cdot \sin(\frac{\pi}{6}) + \cos^2(\frac{\pi}{3})\)
1. Potęgowanie i logarytm
Pierwszy krok to obliczenie \(3^3\), co daje nam 27. Następnie obliczamy logarytm \(\log_{10}(100)\), który jest równy 2, ponieważ \(10^2 = 100\). Jest to przykład wykorzystania logarytmów do przekształcania potęg w proste mnożniki.
2. Dzielenie
W tym kroku sumujemy wyniki z pierwszego kroku, czyli \(27 + 2 = 29\), a następnie dzielimy przez 27, co daje nam \(\frac{29}{27}\).
3. Sinus i cosinus
Obliczamy \(\sin\left(\frac{\pi}{6}\right)\), który wynosi 0.5, co odpowiada wartości sinusa dla kąta 30 stopni (w radianach \(\frac{\pi}{6}\)). Następnie obliczamy \(\cos^2\left(\frac{\pi}{3}\right)\), co daje 0.25. Wynika to z faktu, że \(\cos\left(\frac{\pi}{3}\right)\) wynosi 0.5, a jego kwadrat to właśnie 0.25.
4. Końcowe obliczenia i wynik
Teraz mnożymy \(\frac{29}{27}\) przez wynik sinusa (0.5) i dodajemy do tego wynik cosinusa kwadrat (0.25), aby otrzymać końcowy wynik działania.
Ostateczny wynik
To dziłanie pokazuje, jak łączyć różne elementy matematyczne, takie jak dzielenie, funkcje trygonometryczne i dodawanie, aby uzyskać ostateczny wynik.
Ostateczny wynik tego zaawansowanego działania matematycznego to ≈0.787.