Co to jest funkcja liniowa?
Funkcja liniowa jest jednym z najprostszych typów funkcji matematycznych. Ma ona postać: [ y = ax + b ]
gdzie:
- ( y ) to wartość funkcji (zależna),
- ( x ) to zmienna niezależna,
- ( a ) to współczynnik kierunkowy prostej,
- ( b ) to wyraz wolny, który przesuwa wykres funkcji w górę lub w dół.
Współczynnik kierunkowy i wyraz wolny
- Współczynnik Kierunkowy ( a ): Określa on nachylenie prostej. Jeśli ( a > 0 ), prosta jest nachylona do góry, jeśli ( a < 0 ) – nachylona do dołu. Jeżeli ( a = 0 ), mamy do czynienia z funkcją stałą (prostą równoległą do osi X).
- Wyraz Wolny ( b ): Wskazuje, w którym miejscu prosta przecina oś Y. Na przykład, jeśli ( b = 3 ), prosta przetnie oś Y w punkcie (0, 3).
Rysowanie wykresu funkcji liniowej krok po kroku
- Znajdź punkt przecięcia z osią Y: To będzie punkt, gdzie ( x = 0 ). Wstaw ( x = 0 ) do równania i znajdź ( y ).
- Użyj współczynnika kierunkowego: Aby znaleźć drugi punkt, wybierz dowolną wartość dla ( x ) i oblicz ( y ) korzystając z równania funkcji.
- Narysuj prostą: Połącz te dwa punkty prostą linią. Ta linia to wykres twojej funkcji liniowej.
Przykładowe wykresy
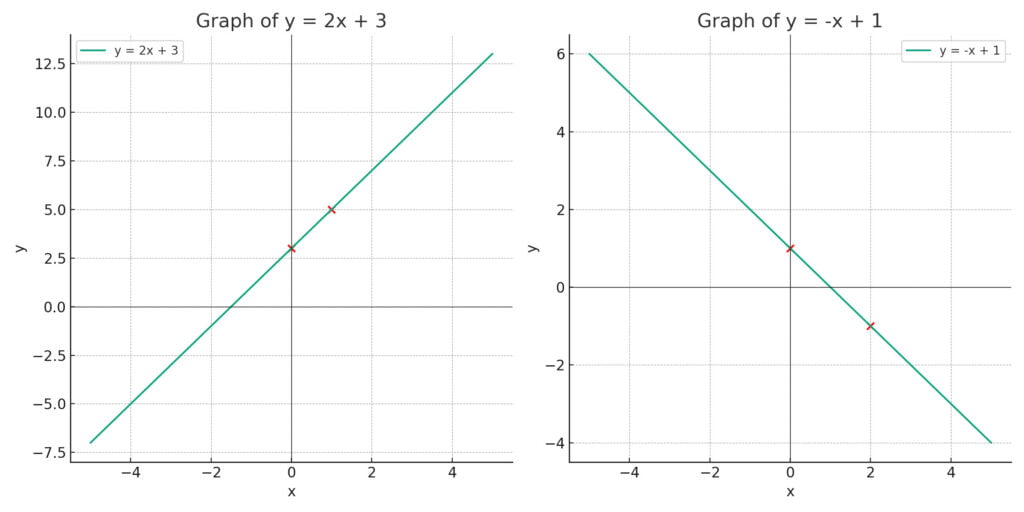
Przykład 1: y = 2x + 3
- Punkt przecięcia z osią Y: dla x = 0, y = 3. Punkt: (0, 3).
- Wybierz x = 1, y = 2*1 + 3 = 5. Drugi punkt: (1, 5).
- Narysuj linię przechodzącą przez (0, 3) i (1, 5).
Przykład 2: y = -x + 1
- Punkt przecięcia z osią Y: dla x = 0, y = 1. Punkt: (0, 1).
- Wybierz x = 2, y = -2 + 1 = -1. Drugi punkt: (2, -1).
- Narysuj linię przechodzącą przez (0, 1) i (2, -1).
W obu przypadkach, kluczowe jest znalezienie dwóch punktów i połączenie ich prostą linią. Im więcej punktów znajdziesz, tym dokładniejszy będzie twój wykres, ale dwa punkty są zazwyczaj wystarczające do narysowania funkcji liniowej.
Miejsce zerowe funkcji
Miejsce zerowe to punkt, gdzie funkcja przecina oś X (czyli y = 0).
Aby je znaleźć, wystarczy przyrównać równanie funkcji do zera i rozwiązać je względem ( x ).
Przykład obliczanie miejsca zerowego funkcji liniowej
Mamy funkcję liniową w postaci:
Krok 1: Ustawienie y na 0
Pierwszym krokiem jest przyrównanie wartości funkcji do zera.
Krok 2: Rozwiązanie równania względem x
Rozwiązujemy równanie, aby znaleźć \( x \). Najpierw dodajemy 6 do obu stron równania:
Co upraszcza się do:
Następnie dzielimy obie strony równania przez 2:
Co daje nam:
Krok 3: Interpretacja wyniku
Znaleźliśmy, że \( x = 3 \) jest miejscem zerowym naszej funkcji liniowej. Oznacza to, że wykres funkcji \( y = 2x – 6 \) przecina oś X w punkcie (3, 0).
Odpowiedź:
Miejsce zerowe funkcji liniowej \( y = 2x – 6 \) wynosi \( x = 3 \). W praktyce oznacza to, że gdy podstawimy \( x = 3 \) do równania naszej funkcji, wartość \( y \) będzie równa zero. To jest punkt, w którym nasza prosta przecina oś X na wykresie.
Pamiętaj, że praktyka jest kluczem do zrozumienia funkcji liniowej. Ćwicz rysowanie różnych wykresów funkcji liniowych, zmieniając wartości współczynników ( a ) i ( b ), aby zobaczyć, jak wpływają one na kształt wykresu. Powodzenia! 🌟📉📘
Właściwości funkcji liniowych
- Monotoniczność: Funkcje są rosnące, malejące lub stałe w zależności od współczynnika kierunkowego.
- Stała szybkość zmiany: Szybkość zmian (gradient) jest stała dla każdej funkcji liniowej.
- Przecięcie z osią Y: Wskazuje, gdzie wykres funkcji przecina oś Y.
- Brak ekstremów: Funkcje liniowe nie mają maksimów ani minimów.
- Prosta jako wykres: Wykres każdej funkcji liniowej jest prostą.
- Zastosowania praktyczne: Są szeroko stosowane w różnych dziedzinach, takich jak ekonomia czy inżynieria.
- Symetria: Symetria względem prostej przechodzącej przez punkt przecięcia z osią Y.
- Zależność od współczynników: Wartości współczynników wpływają na kształt i położenie wykresu.
Rodzaje zadań funkcji liniowej
Zadania z funkcji liniowej mogą przybierać różne formy, od prostych pytań wymagających podstawowej wiedzy, po bardziej skomplikowane problemy zastosowujące tę wiedzę w praktyce. Oto kilka przykładów zadań na sprawdzianach, które mogą pojawić się w kontekście nauki o funkcji liniowej:
- Znajdowanie współczynników: Dana jest funkcja liniowa w postaci ( y = ax + b ). Uczniowie mogą być poproszeni o określenie współczynników ( a ) (współczynnik kierunkowy) i ( b ) (wyraz wolny) na podstawie podanego równania lub wykresu.
- Rysowanie wykresu funkcji: Uczeń otrzymuje równanie funkcji liniowej i musi narysować jej wykres. Może to obejmować znalezienie dwóch lub więcej punktów, przez które przechodzi wykres, a następnie połączenie ich prostą linią.
- Obliczanie miejsca zerowego: Zadaniem jest znalezienie miejsca zerowego funkcji liniowej, czyli wartości ( x ), dla której ( y = 0 ).
- Rozwiązywanie nierówności liniowych: Uczeń musi rozwiązać nierówność liniową, taką jak ( 3x + 2 > 5 ), i przedstawić rozwiązanie na osi liczbowej lub w postaci przedziału.
- Zastosowanie w problematyce słownej: Zadanie polega na zastosowaniu funkcji liniowej do rozwiązania problemu słownego, na przykład obliczeniu kosztów, prędkości, czy innych wielkości związanych z ruchem jednostajnie prostoliniowym.
- Porównywanie funkcji liniowych: Uczeń może zostać poproszony o porównanie dwóch lub więcej funkcji liniowych, na przykład w kwestii nachylenia, punktów przecięcia, czy zakresu wartości.
- Znajdowanie punktów przecięcia: Uczniowie mogą otrzymać zadanie znalezienia punktu lub punktów przecięcia dwóch funkcji liniowych.
- Interpretacja kontekstowa: Odczytywanie i interpretowanie informacji przedstawionych w postaci wykresu funkcji liniowej, na przykład w kontekście danych ekonomicznych czy naukowych.
Te przykłady pokazują, jak różnorodne i wszechstronne mogą być zadania związane z funkcją liniową, od prostych obliczeń po zastosowania w rzeczywistych scenariuszach.
Gdzie w życiu i praktyce wykorzystujemy funkcje liniowe?
Funkcje liniowe znajdują zastosowanie w wielu aspektach codziennego życia oraz w różnych dziedzinach nauki i techniki. Oto kilka przykładów, które pokazują, jak szeroko wykorzystywane są one w praktyce:
- Ekonomia i finanse: Funkcje liniowe są używane do modelowania różnych sytuacji ekonomicznych, takich jak obliczanie procentów, kosztów, przychodów, czy zysków. Na przykład, jeśli koszt produkcji jednostki produktu wzrasta liniowo w zależności od ilości wyprodukowanych jednostek, możemy użyć funkcji liniowej do obliczenia całkowitego kosztu produkcji.
- Fizyka: W fizyce, szczególnie w kinematyce, funkcje liniowe są wykorzystywane do opisania ruchu jednostajnego prostoliniowego, gdzie prędkość jest stała, a przebyta droga zmienia się liniowo w czasie.
- Budownictwo i inżynieria: W budownictwie, funkcje liniowe mogą być używane do projektowania elementów konstrukcyjnych, np. w obliczeniach związanych z obciążeniem czy gradientami nachylenia.
- Statystyka i analiza danych: Funkcje liniowe są podstawą w prostych modelach regresji liniowej, które służą do analizowania i przewidywania związków między zmiennymi. Na przykład, mogą pomóc w przewidywaniu sprzedaży na podstawie wydatków na reklamę.
- Gospodarstwo domowe: Proste obliczenia związane z planowaniem budżetu domowego czy wyznaczaniem kosztów zużycia energii czy wody często opierają się na liniowych zależnościach.
- Informatyka: Algorytmy komputerowe, szczególnie te związane z analizą i przetwarzaniem danych, często korzystają z funkcji liniowych do modelowania złożoności czasowej.
- Medycyna: W dawkowaniu leków, funkcje liniowe mogą być używane do obliczenia odpowiedniej dawki leku w zależności od wagi pacjenta.
- Grafika komputerowa: Funkcje liniowe są używane w grafice komputerowej, na przykład w skalowaniu obrazów czy animacji.
- Planowanie trasy i nawigacja: Wyznaczanie najprostszej, liniowej trasy między dwoma punktami na mapie to przykład wykorzystania funkcji liniowej.
- Handel i sprzedaż: Ustalanie cen, marż, czy rabatów jest często oparte na prostych zależnościach liniowych.
Te przykłady pokazują, że funkcje liniowe są nie tylko abstrakcyjnym konceptem matematycznym, ale mają praktyczne zastosowanie w wielu różnych dziedzinach życia.