Obliczanie współczynnika kierunkowego prostej
Obliczenie współczynnika kierunkowego prostej, często oznaczonego jako \(a\) w kontekście równania linii prostej \(y = ax + b\), jest kluczowym krokiem w analizie własności linii prostej na płaszczyźnie. Współczynnik ten wyraża nachylenie prostej względem osi X i określa, jak szybko zmienia się wartość \(y\) (wysokość) w miarę zmiany wartości \(x\) (szerokość).
Jak obliczyć współczynnik kierunkowy \(a\):
Dla prostej przechodzącej przez dwa punkty:
Jeśli mamy dane dwa punkty przez które przechodzi prosta, \(P_1(x_1, y_1)\) i \(P_2(x_2, y_2)\), współczynnik kierunkowy \(a\) można obliczyć korzystając z następującej formuły:
Ta formuła jest bezpośrednim wynikiem definicji współczynnika kierunkowego jako miary zmiany wartości \(y\) w stosunku do zmiany wartości \(x\).
Interpretacja współczynnika kierunkowego:
- \(a > 0\): Prosta jest nachylona “w górę” w kierunku prawej strony układu współrzędnych, co oznacza, że wartości \(y\) rosną wraz ze wzrostem wartości \(x\).
- \(a < 0\): Prosta jest nachylona "w dół" w kierunku prawej strony układu współrzędnych, co oznacza, że wartości \(y\) maleją wraz ze wzrostem wartości \(x\).
- \(a = 0\): Prosta jest równoległa do osi X i nie ma nachylenia (jest to prosta pozioma).
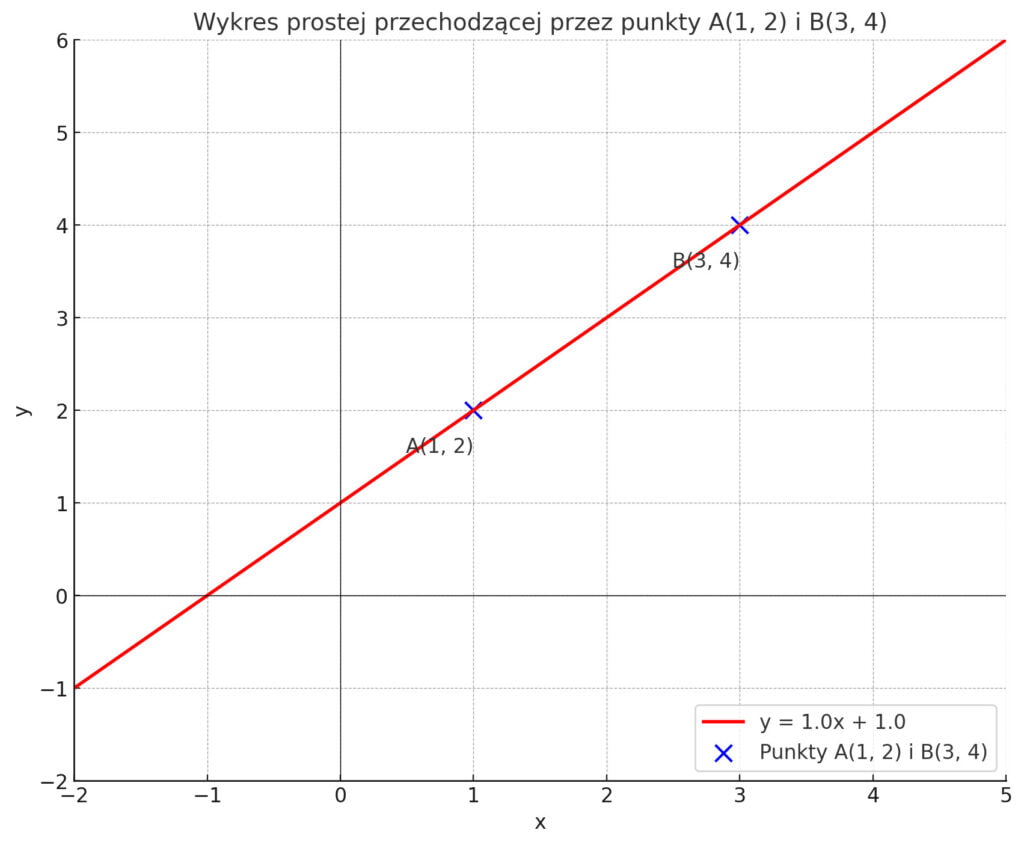
Przykład:
\(a = \frac{4 – 2}{3 – 1} = \frac{2}{2} = 1\)
To oznacza, że prosta przechodząca przez te punkty jest nachylona pod kątem, który odpowiada współczynnikowi kierunkowemu równemu 1, sugerując, że dla każdego kroku w prawo (wzrost \(x\) o 1), wartość \(y\) również wzrasta o 1.
Przykład 1: Wyznaczenie współczynnika kierunkowego
Jak znaleźć współczynnik kierunkowy prostej przechodzącej przez punkty \(A = (2, 3)\) i \(B = (-1, -2)\)?
Krok po kroku rozwiązanie:
- Wzór na współczynnik kierunkowy: \( a = \frac{y_B – y_A}{x_B – x_A} \). Jest to podstawowa zasada obliczania nachylenia prostej, uwzględniająca różnice współrzędnych punktów.
- Podstawienie wartości punktów: \( a = \frac{-2 – 3}{-1 – 2} \). Tutaj wstawiamy współrzędne danych punktów do wzoru.
- Wykonanie obliczeń: Po prostym przekształceniu arytmetycznym otrzymujemy \( a = \frac{-5}{-3} \).
- Uproszczenie wyniku: Skracając ułamek, dochodzimy do \( a = \frac{5}{3} \), co jest ostatecznym wynikiem.
Wynik: Współczynnik kierunkowy prostej wynosi \( a = \frac{5}{3} \), co oznacza, że prosta jest nachylona pod kątem, którego tangens wynosi \( \frac{5}{3} \).
Przykład 2: Wyznaczenie współrzędnych punktów na prostej
Wyznaczamy współrzędne punktów na prostej o współczynniku kierunkowym równym \(\frac{3}{2}\), przechodzącej przez punkt \(A = (2, -3)\).
Krok po kroku rozwiązanie:
- Wzór na współczynnik kierunkowy: \( a = \frac{y_B – y_A}{x_B – x_A} \). Jest to podstawowa zasada obliczania nachylenia prostej, uwzględniająca różnice współrzędnych punktów \(A = (x_A, y_A)\) i \(B = (x_B, y_B)\).
- Podstawiając do wzoru współczynnika kierunkowego wartości punktów \(A = (2, -3)\) oraz przyjmując współczynnik kierunkowy \(a = \frac{3}{2}\), otrzymujemy równanie prostej w postaci punktowo-kierunkowej: \(y – y_A = a(x – x_A)\).
- Podstawiając dane: \(y + 3 = \frac{3}{2}(x – 2)\), co po przekształceniu daje (mnożymy przez 2, obie strony w celu redukcji ułamka): \(2(y + 3) = 3(x – 2)\).
- Rozwijając równanie: \(2y + 6 = 3x – 6\), a następnie przekształcając do postaci ogólnej: \(2y – 3x = – 12\) | \(2y = 3x – 12\) .
- Dzieląc obie strony przez 2, otrzymujemy równanie w postaci \(y = \frac{3}{2}x – 6\), które pozwala na łatwe wyznaczenie współrzędnych \(y\) dla dowolnych wartości \(x\).
- Przykładowe obliczenia współrzędnych punktów na prostej pokazują, że punkty \((2, -3)\), \((4, 0)\), i \((6, 3)\) leżą na prostej o współczynniku kierunkowym \(\frac{3}{2}\).
Wynik: Punkty \((2, -3)\), \((4, 0)\), i \((6, 3)\) leżą na prostej o współczynniku kierunkowym \(\frac{3}{2}\), co potwierdza zgodność z początkowymi założeniami.