Analiza ruchu windy. Zadanie z fizyki, kinematyka

Pytanie i treść zadania

Określ czas wznoszenia się windy, zakładając, że jej ruch podczas ruszania i hamowania jest jednostajnie zmienny o przyspieszeniu równym, co do wartości bezwzględnej, \(a = 1 \, \text{m/s}^2\), a na środkowym odcinku drogi ruch jest jednostajny z szybkością \(v = 2 \, \text{m/s}\). Wysokość, na którą wznosi się winda, to \(h = 60 \, \text{m}\). Sporządź wykres prędkości windy od czasu trwania jej ruchu.

Zebranie danych:

• Przyspieszenie \(a = 1 \, \text{m/s}^2\)
• Prędkość na środkowym odcinku \(v = 2 \, \text{m/s}\)
• Wysokość wzniesienia \(h = 60 \, \text{m}\)

Wzory:

Analiza ruchu windy

W zadaniu analizujemy ruch windy, który składa się z trzech etapów: przyspieszania, ruchu jednostajnego oraz hamowania. Przyspieszenie \(a\) i hamowanie mają wartość \(1 \, \text{m/s}^2\), ruch jednostajny odbywa się z prędkością \(2 \, \text{m/s}\), a całość ma na celu pokonanie wysokości \(60 \, \text{m}\).

Metodologia

Podział procesu na etapy pozwala na osobne obliczenie czasu i drogi dla każdego z nich, a następnie na sumowanie wyników w celu uzyskania całkowitego czasu wznoszenia.

Wyjaśnienie i obliczenia:

1. Faza przyspieszania:

Czas potrzebny do osiągnięcia prędkości \(v\): \(t_1 = \frac{v}{a} = \frac{2 \, \text{m/s}}{1 \, \text{m/s}^2} = 2 \, \text{s}\)

Droga pokonana podczas przyspieszania: \(s_1 = \frac{1}{2} a t_1^2 = \frac{1}{2} \times 1 \, \text{m/s}^2 \times (2 \, \text{s})^2 = 2 \, \text{m}\)

2. Faza ruchu jednostajnego:

Droga ruchu jednostajnego: \(s_3 = h – 2 \times s_1 = 60 \, \text{m} – 2 \times 2 \, \text{m} = 56 \, \text{m}\)

Czas ruchu jednostajnego: \(t_3 = \frac{s_3}{v} = \frac{56 \, \text{m}}{2 \, \text{m/s}} = 28 \, \text{s}\)

3. Faza hamowania:

(Podobnie jak faza przyspieszania)

4. Całkowity czas ruchu:

Całkowity czas: \(T = 2 \times t_1 + t_3 = 2 \times 2 \, \text{s} + 28 \, \text{s} = 32 \, \text{s}\)

Wnioski / odpowiedź

Całkowity czas, w którym winda osiąga pożądaną wysokość, wynosi 32 sekundy. Proces ten składa się z przyspieszenia, ruchu jednostajnego oraz hamowania, gdzie każdy z etapów ma kluczowe znaczenie dla osiągnięcia celu. Ruch windy składa się z trzech etapów: przyspieszania przez 2 sekundy, ruchu jednostajnego przez 28 sekund, i hamowania przez kolejne 2 sekundy.

Wykres prędkości windy

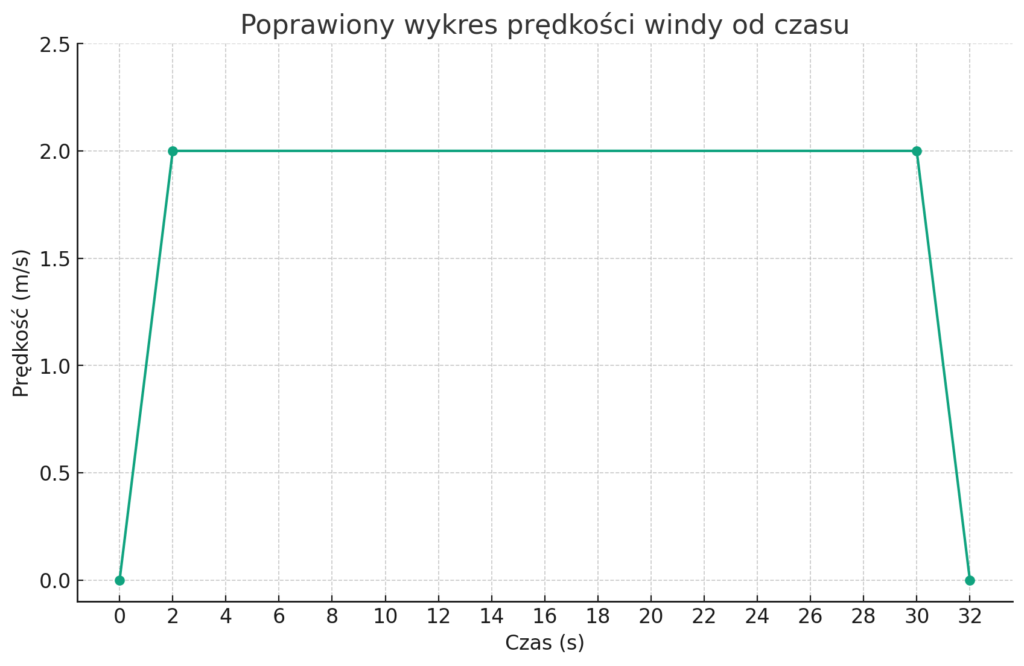
Analiza i problemy

Podczas analizy kluczowe było zrozumienie, że ruch windy można podzielić na trzy charakterystyczne fazy, gdzie każda z nich wymaga zastosowania odpowiednich wzorów fizycznych. Trudnością mogło być prawidłowe określenie, jak długo trwa każdy z etapów oraz jakie odległości są w nich pokonywane. Jednak dzięki metodycznemu podejściu i zastosowaniu podstawowych zasad kinematyki, możliwe było dokładne rozwiązanie problemu.

Analogia:

Wyobraź sobie rowerzystę, który zaczyna jazdę. Najpierw musi pedałować mocniej, aby nabrać prędkości (przyspieszanie), następnie może jechać spokojnie na stałej prędkości (ruch jednostajny), a kiedy chce się zatrzymać, musi zacząć hamować (hamowanie), aby ostatecznie zatrzymać się bezpiecznie. To podobne do etapów ruchu windy: przyspieszenie, ruch z stałą prędkością, i hamowanie.